欧拉定理的应用：Counting regions

Counting regions

Niuniu likes mathematics. He also likes drawing pictures. One day, he was trying to draw a regular polygon with n vertices. He connected every pair of the vertices by a straight line as well. He counted the number of regions inside the polygon after he completed his picture. He was wondering how to calculate the number of regions without the picture. Can you calculate the number of regions modulo 1000000007? It is guaranteed that n is odd.

在图论里有这样一个定理：

对于一个平面图，顶点数-边数+面数=2

我最早看到这个式子是在浙大的高中数学竞赛书中，最近离散数学课也推到图论了，里面讲到了这场多校赛的两个基础知识点，欧拉定理和哈密顿图。

我当时只知道，n阶完全图的边数为C(n,2)，欧拉公式只适用于立体图；

一开始想找找规律，wa了两发；

后来我想，如果把完全图看作一个立体图，也就是说n阶完全图还有一个由外围的n个点形成的面。

这样我们要求的区域数再+1就是立体图的面数；

到这里只需要分别求出顶点数和边数就能带式子了：

顶点数：我们可以这么想每一个内部的交点都是由两条线相交构成的，这个线的两端点是从外面一圈点中选的，那么内部的交点数就相当于从外围的个点中选四个数，构成两条线，两条线再构成一个交点，即交点数为C(n,4)，然后还要加上外围的n个点，所以顶点数为C(n,4)+n；

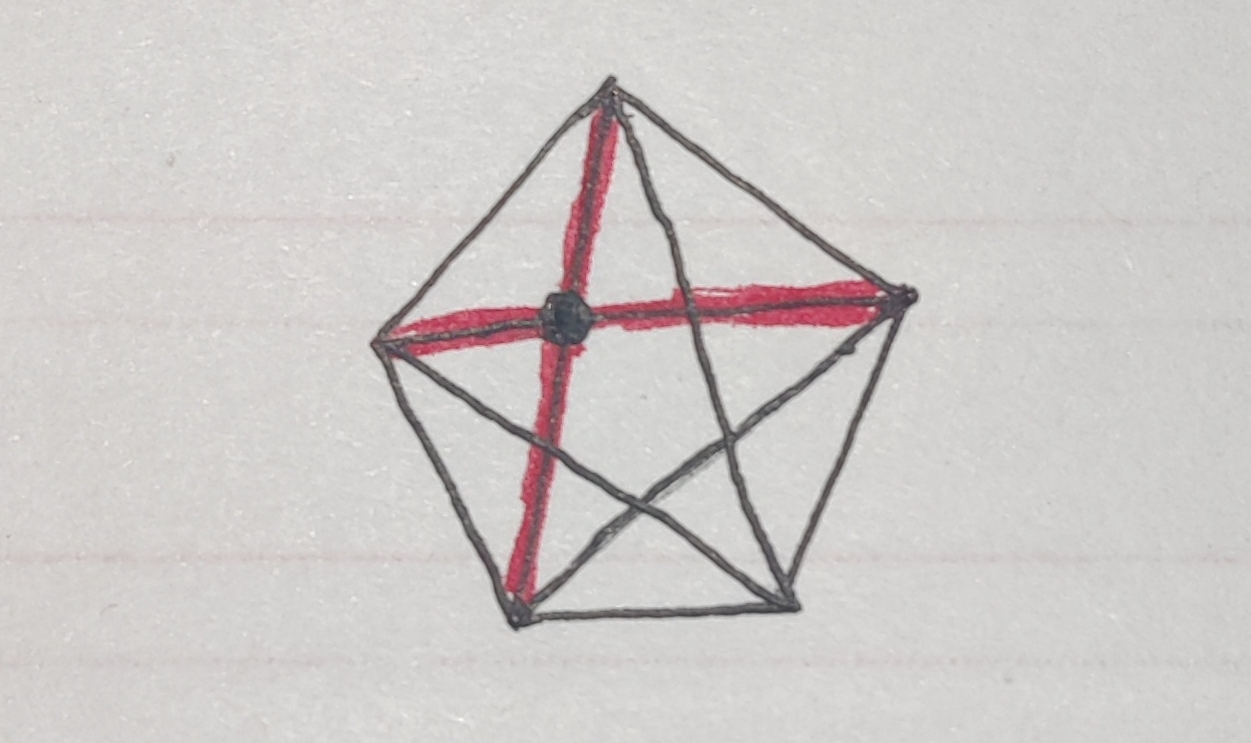
边数：尤其要注意的是，对角线之间互相切割的线段才是边，我们首先知道n阶完全图的边数是C(n,2)，同时我们注意到上图中每形成一个交点都会使两条对角线互相切割，切割成了4段，也就是比原边数多了两段，也就是交点数 2，即C(n,4) 2，然后再把C(n,2)加上就行了，于是边数也就是C(n,4) * 2+C(n,2)；

带入公式：

C(n,4)+n-C(n,4) * 2-C(n,2)+x=2;

x=qu+1;

于是求得

qu=C(n,4)+1-n;

接下来用组合数求就行了；

当然要用到费马小定理求逆元，就不再赘述了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M=1e9+7;
ll qmi(ll a,ll k,ll p){
    ll res=1;
    while(k){
        if(k&1)res=(ll)res*a%p;
        a=(ll)a*a%p;
        k>>=1;
    }
    return res;
}
int C(int a,int b,int p){
    if(a<b) return 0;
    ll x=1,y=1;
    for(int i=a,j=1;j<=b;i--,j++){
        x=(ll)x*i%p;
        y=(ll)y*j%p;
    }
    return x*(ll)qmi(y,p-2,p)%p;
}
int lucas(ll a,ll b,int p){
    if (a<p&&b<p) return C(a,b,p);
    return (ll)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main()
{
	ll n;
	cin>>n;
	cout<<(((C(n,2,M)%M+C(n,4,M)%M)%M)%M+(1-n+M)%M)%M;
	return 0;
}

这着实是个好题，但不太正经。。。